Introduction

The magnetic Skyrmion is a particular configuration of magnetisation vectorfield. Two types of Skyrmion configurations are shown on the Wikipedia magnetic Skyrmion page:

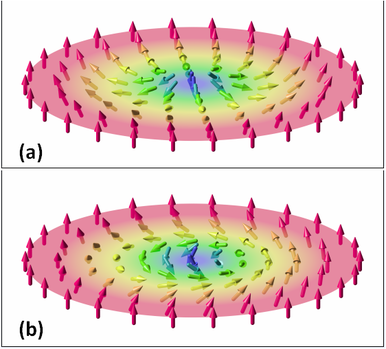
Configuration (a) is sometimes called a radial Skyrmion and (b) is sometimes called a chiral skyrmion to distinguish it from (a). Both have a skyrmion number of 1, and can be observed in different magnetic systems. If we follow a line of vector arrows from the circumference through the centre of the disk to the other side, we see a spiral rotation of the vectors (in a Neel or Bloch domain wall style). We explain the origin of this spiral below.

Skyrmions can be found in magnetic materials that exhibit the Dzyaloshinskii-Moriya Interaction (DMI). Let's start by reviewing the fundamental aspect of a ferromagnetic material, before introducing the DMI.

Ferromagnetic Materials

Ferromagnetic materials are widely known and used, in applications ranging from compass needles to magnetic door locks, in data storage devices such as tapes (yes, they are still used in 2015!) and hard disks.

Ferromagnets exhibit as a key ingredient the so-called (symmetric) exchange interaction: a quantum mechanical effect originating from overlap of the electron's wavefunctions at neighbouring atoms in the crystal atomic lattice. As a result, the magnetic moments (associated with the spin $\vec{s}$ of the wavefunctions) of neighbouring atoms want to point in the same direction to minimise their energy. This exchange interaction energy can be described fairly well through a term like $H_\mathrm{exchange}= - J \vec{s}_1 \vec{s}_2$. This energy $H_\mathrm{exchange}$ is smallest if $\vec{s}_1$ and $\vec{s}_2$ point in the same direction (parallel), and highest if they are antiparallel (for J>0).

Dzyaloshinskii-Moriya Interaction (DMI)

The new kid on the block of interactions in magnetic materials is the Dzyaloshinskii-Moriya Interaction (DMI), also known as asymmetric exchange. It's energy can (in a first approximation) be described as $H_\mathrm{dmi} = \vec{D}_{12} \cdot \vec{s}_1 \times \vec{s}_2$ with a DMI vector $\vec{D}_{12}$ depending on the magnetic system and magnetic moments $\vec{s}_1$ and $\vec{s}_2$. This DMI interaction energy is minimised if (i) there is an angle of 90 degrees between $\vec{s}_1$ and $\vec{s}_1$, and (ii) the angle is oriented such that the cross product $\vec{s}_1 \times \vec{s}_2$ develops a negative sign. The latter feature introduces a preferred sense of rotation (also called chirality or handedness). The DMI energy term tends to align spins $\vec{s}_1$ and $\vec{s}_1$ so that the plane containing them is perpendicular to the DMI vector $\vec{D}_{12}$. This is the reason why two different skyrmion types (radial and chiral) exist, depending on the direction of DMI vector.

Putting the ferromagnetic interaction and the DMI interaction together promises to deliver something interesting: they are both short-range (acting only on nearest neighbours, at least in the model considered here), and they directly compete against each other. It can be shown (or simulated) that the configuration that minimises the energy develops a spiral: a compromise between 90 degree angles and parallel alignment. The curvature of the spiral depends on the relative strength of the interactions (i.e. the ratio $D/J$). Here is such a spiral configuration for a one dimensional chain of magnetic moments:

Skyrmions

In magnetic systems in 2 and 3 dimensions, other configurations are possible, including that knows as a 'Skyrmion' configuration, one of which is shown here:

Skyrmions can arrange in a hexagonal lattice (a skyrmion solid), or move freely (a skyrmion gas) as shown here:

Ongoing research

The possibility to create and manipulate Skyrmions, and the DMI interaction in more general, has raised lots of research interests, including

• Stability of the skyrmions: what anisotropy, applied field and temperature is required to obtain 'stable skyrmions'?
• Statics and dynamics of skyrmions in constrained geometries (such as their stability and field driven reversal in nanodisks and microwave driven reversal
• the ability to drive domain walls with magnons in materials with DMI
• the possibility to create a Skyrmion racetrack memory (see gentle introduction here )

[Note that the above list is biased towards publications from Southampton.]

Oh, the complexity ...

Research into ferromagnetic materials has entertained many thousand scientists and engineers for centuries, and the interactions driving the physics in all magnetic materials, devices and products is dominated by

• the isotropic exchange interaction (short-range, favouring parallel alignment)
• the crystal anisotropy (local, makes certain lattice direction favourable on unfavourable)
• the demagnetisation effect (long-range dipolar interaction, favours flux closure, leading to magnetic domains)
• the effects of external fields (local)
• and other effects, including multi-physics phenomena such as magnetostriction, interaction with currents, and more

This set of competing interactions results in complex systems with many local energy minima and the associated rich statics and dynamics — interesting from a fundamental science point of view and fruitful for technological applications.

The DMI interaction introduces a new (strong and short-range) interaction into this intriguing mix of physics; opening up new challenges to understand fundamental behaviour and paving the path towards unanticipated applications.

It is this background, that — in my eyes — excites the community about magnetic materials with DMI and promises rich physics to be discovered and understood.

In particular, we find the Skyrmion field configuration in the magnetisation vector field in DMI materials. The interpretation of Skyrmions as particles raises questions about the behaviour of Skyrmion matter, adding its own set of research questions within the wider research area of ferromagnetic materials with DMI.