Table of contents
Introduction
What are the crucial simulation methods and software engineering tools computational scientists and engineers need to carry out computer simulations? In this post, I explain the centre directors' motivation behind the choice of the taught programme of our 4-year doctoral training programme in Next Generation Computational Modelling (NGCM).
Context: Centre for Doctoral Training in Next Generation Computational Modelling
The official name of the doctoral training centre is EPSRC Centre for Doctoral Training in Next Generation Computational Modelling (NGCM). This centre offers a 4-year doctoral training programme which is often called an "integrated PhD programme"; meaning that the first year is broadly comparable to a Master of Science which is followed by a 3-year research project. On successful completion of all parts of the 4-year programme, a PhD degree is awarded.
The NGCM training centre is unique in the United Kindgom, and focuses on providing a broad training for those interested in computational science and engineering, bringing together existing best practice from computer science and computational science. The first year is mostly taught, and students carry out a 3-year PhD project in years 2, 3, and 4 that pushes the boundaries of knowledge in simulation development and exploitation of emerging hardware, digging deep into a particular research field, which leads to the PhD thesis.
What motivates the choice of learning content during year one? How can we cater for a range of students from engineering, physics, mathematics, computer science, medicine and chemistry that we expect to carry out computational modelling research and applied simulation in fields as diverse as ab-initio materials modelling, finite-element biomedical implant modelling and bioinformatics?
Simulation Methods
There are a number of simulation techniques that are very widely used, both in the sense of being used by many people in computational science and engineering but also using a large part of the CPU hours on compute facilities such a the UK's national supercomputer ARCHER.
These important simulation methods include finite element and finite difference methods to solve partial differential equations, that arise in many areas of science and engineering, including the well known example of computational fluid dynamics. Dynamic systems ranging from population growth to aircraft altitude control are described by ordinary differential equations, in some fields coupled with noise terms leading to stochastic differential equations.
In Condensed Matter Physics, Chemistry, Material Science and Engineering, ab-initio density functional methods, are used to determine properties of molecules and matter from first principles. At slightly larger length scales, Molecular Dynamics is the tool of choice to study many-particle dynamics, supported by Monte Carlo methods, which have a wider range of applicability.
In modelling more complex processes, such as the flow of products through a factory, supply chains and whole product lifecycles, discrete event methods are used. Related are agent-based models which tend to be used more in simulation of biological or social system with interacting objects.
For each of the methods highlighted in the above paragraphs, we provide an introduction and practical exercises as part of the NGCM training programme, so that every students has heard of these methods, has a feel for their area of applicability and relative merits. No doubt, further study is required to become an expert in any of those, but we try to broaden the horizon by at least making everyone aware of common simulation methods.
Programming languages
Not many topics are debated as vehemently as the choice of programming languages to use, teach and learn. Our view is that the important thing to understand are the principles behind programming, not the particular language: it is unlikely that the languages that are en-vogue today will be the only important languages in 10, 20 or 30 years time (and therefore well within the careers of the students we educate now). We thus need to learn and teach an approach that allows us to embrace and use new languages that develop and emerge in the future. Furthermore, while we could identify the languages that burn the most CPU cycles, there are always particular research projects and domains that use different and quite unusual tools; again indicating the importance of flexibility and the ability to rapidly learn new approaches for students moving into such fields.
The software engineering process of solving a given problem with computer code can be separated into (i) the understanding of the requirements, the design of the system to solve it (data structures, architectures, algorithms) and the development of a solution in pseudocode (or UML or other diagram styles). Then, there is step (ii) in which this design is implemented in a particular language (and of course tested, maintained etc). The figure below tries to summarise this.
[I should add that a full separation of steps i) and ii) is not possible: the final choice of programming language will affect the design, and agile software engineering methods couple the iterative design process to coding.]
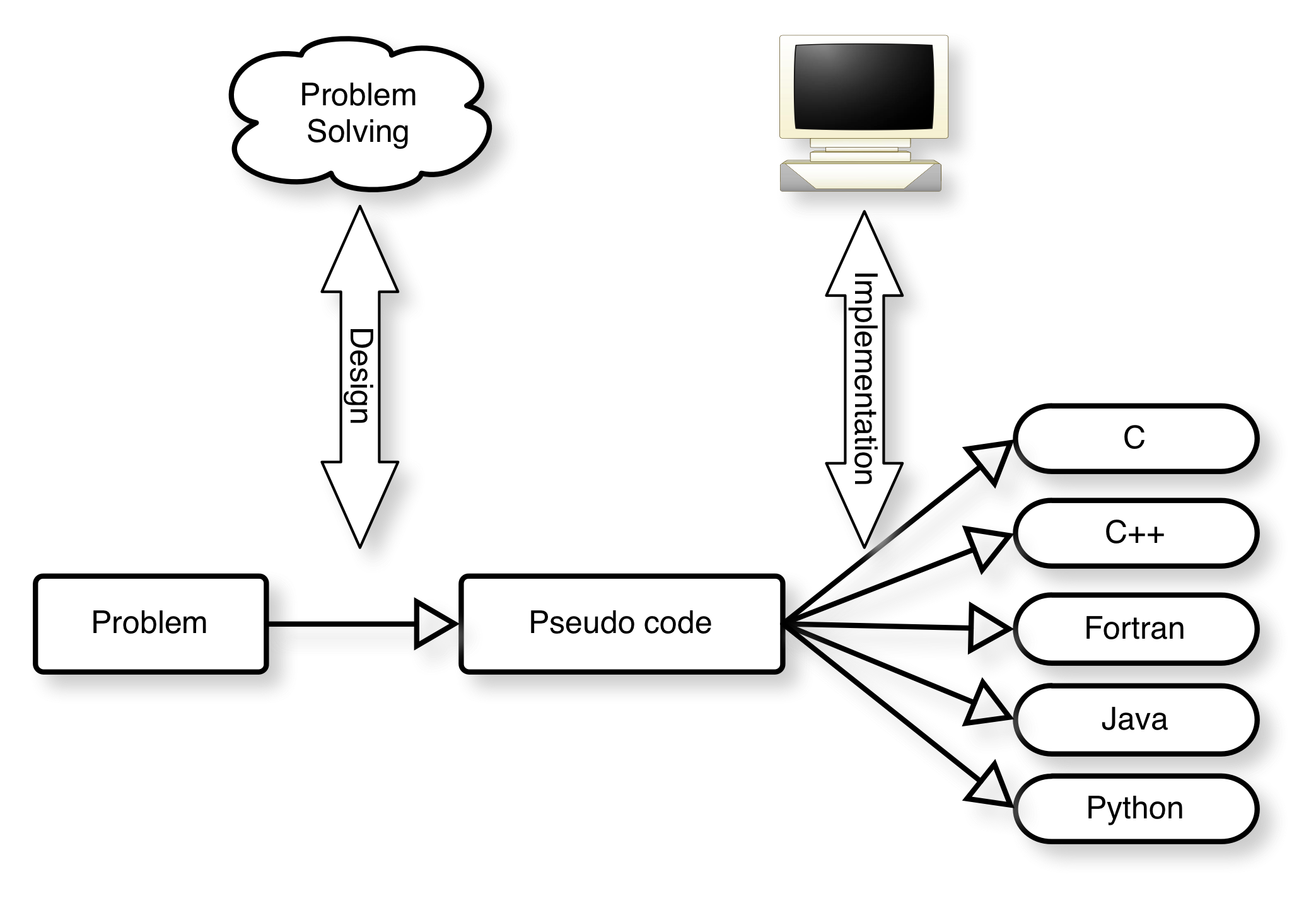
The figure shows programming as a conceptual 2-stage process: (i) finding the algorithmic solution, and (ii) implementing this in a particular language. See also [1].
The strategy is thus to teach ideas and approaches instead of a particular programming language, and thus enabling students to learn further languages as they need to.
Having just explained that "it does not really matter what language we teach", we might as well use languages in our teaching that support the learning of the principles and that are of real immediate and practical value for many of the students where possible.
For our Next Generation Computational Modelling doctoral training programme, we teach the following languages:
Python
Students start the programme with a thorough introduction to Python. We have chosen Python because
- it is a dynamically typed language allowing interactive explorative sessions (something I personally like but which is also key in scientific data exploration),
- Python supports imperative, object oriented and functional programming styles, thus introducing students to all these programming paradigms,
- there is a large and growing set of (scientific and other) Python libraries available (including plotting, matrix operations and standard numerical algorithms).
Python is a versatile language with growing use in computational science and likely to be a main tool for many of our students.
C
We then teach our students the C programming language. We have chosen C because:
- it is statically typed language which can be compiled to fast machine code, and is one of the three main High Performance Computing languages (Fortran, C, C++),
- it is relatively compact language and thus quick to learn (in contrast to C++, say), and well supported by compilers on HPC platforms,
- C code can be combined in a number of ways with Python (ctypes and cython, for example),
- it is useful to understand the basics of C when working in a Linux environment or extracting data from hardware.
If Object Orientation (OO) is required, students can either learn C++ (which is relatively straightforward with the OO experience in Python, and their C knowledge), or combine OO-Python code with C code, where the C code implements only the parts of the code that have to run fast (and these 'fast' routines often don't need OO).
Libraries and tools
A common desire of PhD students is to implement all the code they need, just because they can and because they enjoy programming. And of course academics support this by teaching students the numerical methods that are required to implement a numerical integration scheme. However, there are many high quality libraries out there (including at the numerical level for example BLAS, LAPACK, ODEPACK, MINPACK, FFTW, ...) which are better than what a PhD student could achieve in the short duration of their studies. We thus make the case that code and libraries should be re-used where possible (and similarly, new code should be developed keeping in mind potential re-use by others in the future).
We introduce students to a number of tools such as Emacs, Sublime, Vi, Eclipse, Git, Mercurial, Virtual Machines, IPython/Jupyter, VTK and GUIs for VTK such as Paraview and Mayavi, HDF5, Pandas, to make them aware of those. The depth of some of this introductory learning is limited but by knowing of a tool's existence and some characteristics, students can pick this up immediately when they need to in their PhD research (or later career).
Software Engineering
Computational Science and Engineering research is very often software engineering: the development of new software tools, maintenance and extension of existing tools play central roles.
Software engineering is generally done through 'agile' approaches: let's code something first, see where it gets us to, then re-work, extend etc as required. The absence of long term planning in software engineering for computational science research is likely to be linked to the unpredictability of the first results that are being obtained with the software tool (as this is research).
Many computational scientists and engineers never had the chance to learn software engineering methods to support their software development. We think that the following tools and skills are essential (and reflected in our training programme):
- version control (typically git or mercurial) — it is of highest importance to use version control routinely, to be able to retrieve any earlier version of the code, track down the introduction of bugs, and help make the resulting science reproducible,
- unit, system and regression tests — tests, in particular automatic tests are a huge help in keeping the system error free and allowing refactoring and changes that are inevitable in computational science, test-driven development (TDD) is introduced and encouraged,
- continuous integration — the automatic execution of test, building of documentation and binaries (potentially for different operating systems and library versions) helps in enforcing best practice testing, but is also a motivator for students (and staff!) who like to get the system into a 'clean' state after any changes or extensions.
Statistics
Computer simulations tend to produce a lot of data (some would say 'big data') — imagine a computational fluid dynamics simulation that divides space into a million cells, and then runs a million time steps: the resulting data set will contain a trillion of data points (that's 1012 data points). Assuming each data point contains a velocity vector (3*8 bytes) and a pressure value (1*8 bytes), this is a data set approximately 24TB in size.
The purpose of computing is not numbers but insight, and thus we need to convert this wealth of data into something meaningful. Statistics, postprocessing and visualisation of reduced data sets help us to translate the data that a supercomputer produces into understanding.
Numerical Methods
Where we know the physical laws — such as in physics, chemistry and engineering — a recurring challenge is to solve complicated equations numerically. This has to happen fast and accurately, and we need to know how in accurate our numerical approximations are. Furthermore, the floating point data type introduces numerical errors and we need our algorithms to be robust towards small deviations to deal with this. Numerical mathematics addresses these challenges. While many of the standard numerical challenges (such as root finding and numerical integration) do not need to be implemented in practice as great libraries exist, it is the learning of the ideas and approaches that is important, and which will help students to develop their own algorithms, estimate errors and show convergence.
Summary
The notes above outline the motivation behind our current PhD-level training programme to educate and develop the next generation of computational scientists and engineers at the Southampton EPSRC Centre for Doctoral Training in Next Generation Computational Modelling.
The training programme goes beyond the topics outlined above, including for example soft skills, team working, exposure to a small research project in the summer of the first year before the main 3-year research PhD starts, or – as an option – execution of a small small research project throughout the first year, the NGCM Summer Academy and exposure to computational science in industry through our industry partners.
If you are interested in joining us as a PhD student, have a look at our webpages, blog, the list of available projects or get in touch with any queries. We have fully funded PhD studentships for UK students, and for EU students for many of our projects.
| [1] | H. Fangohr. A Comparison of C, Matlab and Python as Teaching Languages in Engineering, Lecture Notes on Computational Science 3039, 1210-1217 (2004) (preprint) |