Driving domain walls with magnons in DMI materials — Computational Science and Data Science

Summary of our recent PRL on driving domain walls with magnons in the presence of the Dzyaloshinskii-Moriya Interaction (DMI)

Weiwei Wang, Maximilian Albert, Marijan Beg, Marc-Antonio Bisotti, Dmitri Chernyshenko, David Cortes, Ian Hawke, and Hans Fangohr
Magnon driven domain wall motion with the Dzyaloshinskii-Moriya interaction
Physical Review Letters 114, 087203 (2015)
(Online: journal arXiv.org)

Context: Materials with Dzyaloshinskii-Moriya Interaction

A very brief introduction to magnetic materials with Dzyaloshinskii-Moriya Interaction (DMI) is available here.

Summary: Magnons induced domain wall motion — conservation of angular momentum

Domain wall motion Magnons (i.e. spin wave excitations) travelling along a 1d magnetic structure with a domain wall, will move the domain wall a little bit as in demonstrated in the animation above. This happens as angular momentum $\hbar$ of the magnon is transferred to the magnetisation structure as the magnon travels through the domain wall. The spinwave vector $k$ and frequency $\omega$ are not affected.

This paper studies the same process in the presence of DMI interactions, and finds that there is a different mode of momentum transfer: $k$ does change in the process and moves the domain wall faster.

The system in this study

1d model system (in x-direction)
with exchange interaction and
(bulk) DMI interaction
uniaxial anisotropy of strength $K$ with easy axis in x direction
perpendicular anisotropy $K_p$
no demagnetisation field

Experiment

We then carry out the following (simulated) experiment:

put head-to-head domain wall into the centre of the wire
excite spinwaves (i.e. magnons) at given frequency $\omega$ at one end of the wire
measure position and velocity of the domain wall as a function of time

Results, without perpendicular anisotropy (i.e. $K_p = 0$)

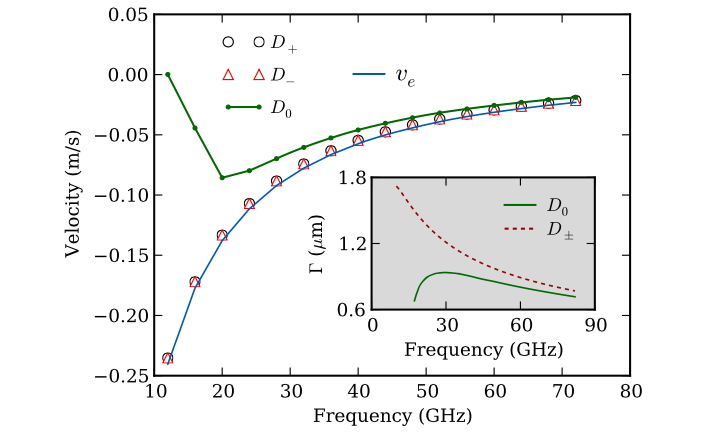
Figure 2 of paper

Figure 2 of the paper. While magnons are travelling down the 1d system, the domain wall starts to move. This figure shows the (steady-state) domain wall velocity as a function of the frequency of the magnons.

The hollow black circle and hollow red triangle labelled $D_+$ and $D_-$ show data points from the simulation with DMI (with posititve and negative sign), the small solid green dots show data points as obtained in the absence of DMI (i.e. $D=0$).

In the (simulated) experiment, we observe:

A small negative velocity (~0.1m/s), i.e. the domain wall moving towards the magnon source.
The same behaviour for negative and positive $D$, and a similar order of magnitude of the domain wall velocity for $D=0$ (i.e. no DMI in the material).

The blue line labelled $v_e$ is an analytical model result describing the data well. It is based on the assumption that the domain wall motion is due to angular momentum transfer, that each magnon carries an angular momentum of $\hbar$, and transfers $2\hbar$ onto the domain wall when travelling through it. The presence of DMI has no significant effect here.

Results, with perpendicular anisotropy (i.e. $K_p > 0$)

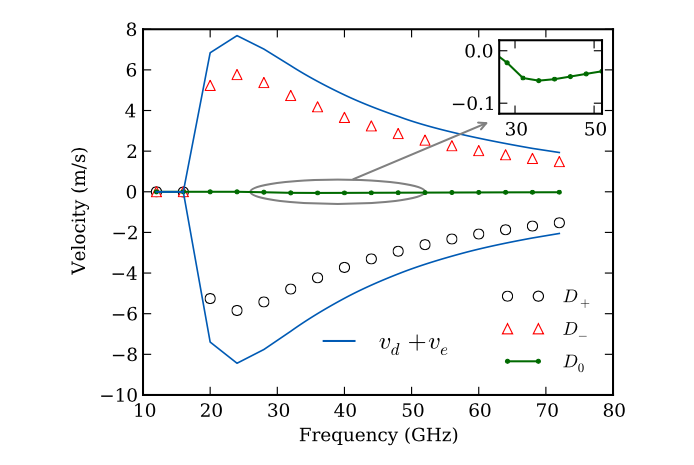
Figure 3 of paper

Figure 3 of the paper. This figure shows the domain wall velocity as a function of the frequency of the magnons in the presence of perpendicular anisotropy (i.e. $K_p > 0$ ).

We observe:

Large velocities ($|v| \sim 5$ m/s) where the velocity is positive for negative $D$ and the velocity is negative for positive $D$. These are 1 to 2 orders of magnitude larger than in the $K_p = 0$ case shown in figure 2.
For $D=0$, the velocity is very small ($\sim 0.05$ m/s), as in figure 2
The curve $v_d$ is the domain wall motion due to linear momentum transfer. The value of $v_e$ in figure 3 is of similar magnitude as $v_e$ in figure 2, and thus $v_d + v_e \approx v_d$.

The interpretation of the data is that the linear moment transfer is $\delta k$ (Fig S2 a in the Supplemental material) and comes from the dispersion relation depending on the magnetisation: for $\vec{m}=(1, 0, 0)$ we get one branch and for $\vec{m}=(-1, 0, 0)$ we get another branch. The frequency $\omega$ does not change much (see Fig S3a in supplemental material) when the magnon passes the domain wall, so $k$ has to change by $\delta k$ as we go from one branch to the other. This effect is only present with DMI and in the additional presence of the perpendicular anisotropy, that suppresses rotation of the domain wall around the x-axis.

Summary of the influence of bulk DMI

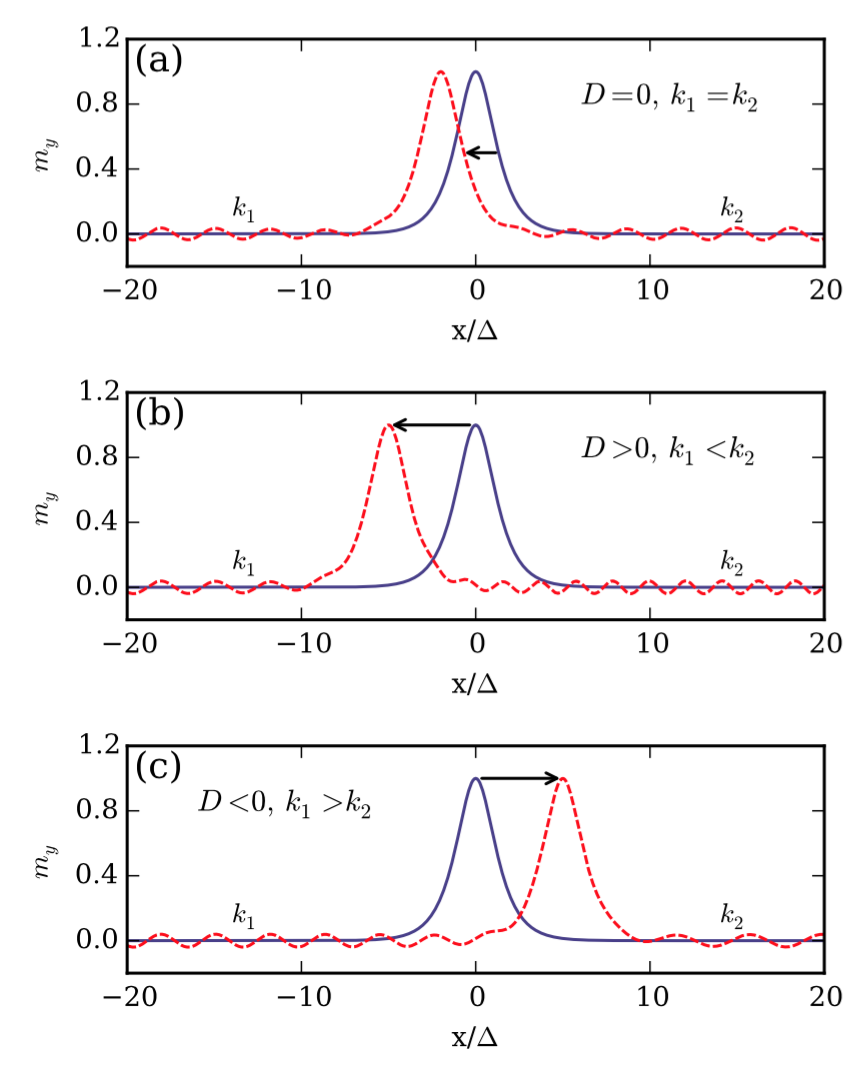Domain wall motion with DMI As we can see, in (a) a domain wall moves to left due to conservation of angular momentum. Without DMI the wave vectors of a magnon before ($k_1$) and after $k_2$ passing through the domain wall remain the same ($k_1=k_2$). In the presence of DMI, the wave vector either increases or decreases, as shown in (b) or (c), which leads to a faster domain wall motion with controllable directions. We attribute this to linear momentum transfer.

Summary

Study magnon driven dynamics in 1d system with DMI
Given perpendicular anisotropy and DMI, the domain wall velocity due to magnons is increased by 1-2 orders of magnitude
Originates in linear momentum transfer

Future work

Magnetisation dynamics is an active field of research - if you are interested to pursue a PhD in computational modelling of such systems, please get in touch.

Full text access and paper details

PDFs are available from:

Related information

A summary of the findings has been give in a Nature Nanotechnology 10 293 (2015) Research Highlight