Summary of a recent publication based on Molecular Dynamics and Monte Carlo simulations of particles, with contributions from University of Massachusetts (US), The Royal Institute of Technology, Stockholm (Sweden), The Pennsylvania State University (US), University of West Florida (US) and the University of Southampton (UK):
Christopher N. Varney and Karl A. H. Sellin and Qing-Ze Wang, and Hans Fangohr and Egor Babaev Hierarchical structure formation in layered superconducting systems with multi-scale inter-vortex interactions, Journal of Physics: Condensed Matter 25, 415702 (2013).
Context
Lennard-Jones potential
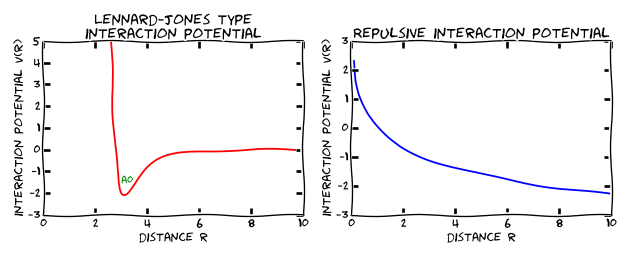
Figure A: (Left) The Lennard Jones potential: the distance A0 is the optimum distance as it has the lowest potential energy. (Right) A purely repulsive potential: particles exposed to this will try to separate from each other as far as possible. We have used arbitrary units on both axes for these schematic plots.
The physics and emergent behaviour of interacting particles has long standing history: classical computational problems include the simulation of the behaviour of many atoms in liquids, solids, proteins etc, and common simulation techniques are Molecular Dynamics and (Metropolis) Monte Carlo methods.
For both, we need to know the pairwise interaction potential between two particles (we ignore here systems that require 3 and more body interactions to be considered).
For example, the well known Lennard Jones potential (shown in Figure A (left) above) for two particles such as inert atoms, has a repulsive term that for short distances R increases the energy (of the type $1/R^{12}$, and an attractive term (of the type $1/R^6$. The first term originates in strong repulsion of electron orbitals that start to overlap, the second in weak attraction from induced electrical polarisation. The two terms combined result in a potential as shown in figure 1a), which has a minimum at a distance A0 (approximately 3 for the schematic sketch): each pair of particles has the lowest possible energy if they can be separated by this distance A0.
Repulsive potential
Another area of complex system research that uses particle-based simulation techniques such as Molecular Dynamics and Monte Carlo methods is that of the the dynamics of vortex lines in (Type II) superconductors. In these systems, the vortex lines always repel each other, and a corresponding potential is shown in figure A (right): for all distances, the energy decreases if we increase the distance between the two interacting objects, separated by a distance R.
In these systems, the vortex lines cannot escape the sample, so that they will arrange in a way to minimise they energy, which is - in the absence of any other disordering effects and absence of geometrical constraints of the sample - a hexagonal lattice.
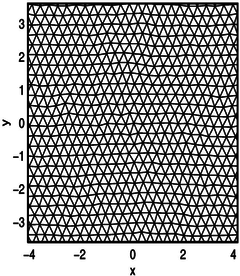
Figure B: Delaunay triangulation of (nearly) hexagonal system of vortices that repel each other with a potential as in Figure A (right). They are also exposed to a small disordering effect that causes the deviation from the perfect hexagonal lattice. [Taken from Figure 5 in Vortex Dynamics in two-dimensional systems at high driving forces (postprint pdf).]
Novelty in this work
Recently, the possibility of more complicated inter-vortex interactions in newly discovered systems (so-called Type 1.5 superconductors) has attracted much attention: in multi-component and multi-layer superconductors the interaction potential:
- can exhibit attractive and repulsive components and
- can have multiple length scales for the repulsion.
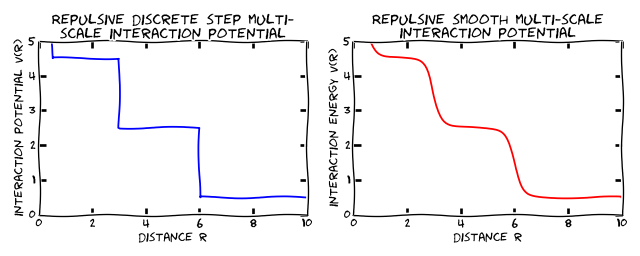
Figure C: (Left) Step potential, repulsive with multiple length scales. (Right) Smoth potential, repulsive with multiple length scales. Figure D shows some results obtained with this class of interaction potentials.
Figure C demonstrates a repulsive potential with multiple length scales: for shortest length scales, the interaction energy is high (although for the discrete function on the left it doesn't matter what the particle separation is as long as the distance is with the range for which the potential is constant), and decreases as the separation increases. The figure on the right shows a physically more realistic potential with smooth rather than discrete step changes.
Selected results
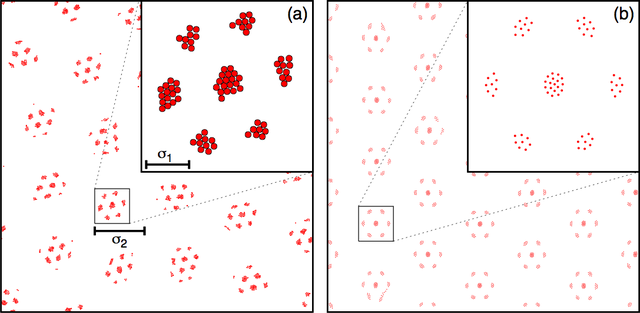
Figure D shows (left) vortex equilibrium configurations for the discrete potential and (right) for the smoothed potential, both figures revealing clusters of vortices that arrange in a hexagonal lattice. The insets show details about each cluster: for the step potential the position of the particles within the same plateau of the step function is irrelevant (left inset) where as for the smooth repulsive potential (right inset) the vortices inside the cluster try to maximise their distance. [This is taken from Figure 2 in publication.]
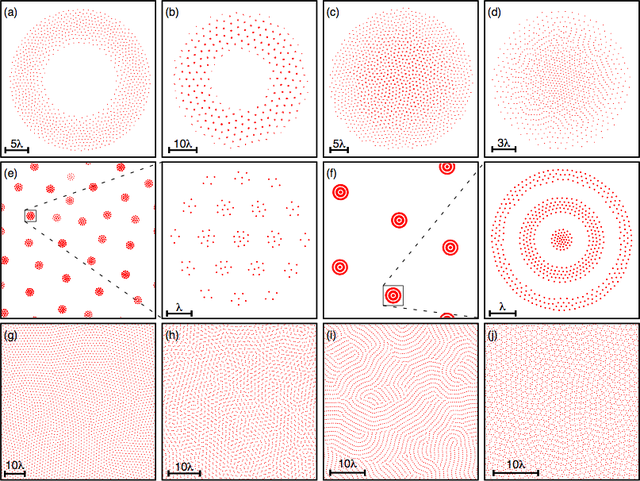
Figure E shows a number of configurations that are obtained for multi-length scale potentials with attractive and repulsive components. [Figure E is taken from figure 4 in publication).]
Summary
- study hierarchical configurations from interactions potentials that
- are repulsive and attractive
- on multiple length scales
- Simulation carried out using Metropolis Monte Carlo simulations and Langevin type dynamics simulation of the vortex state.
Future work
This is an active field of research - if you are interested to pursue a PhD in computational modelling of such systems, please get in touch.
Full text access and paper details
Christopher N. Varney and Karl A. H. Sellin and Qing-Ze Wang, and Hans Fangohr and Egor Babaev Hierarchical structure formation in layered superconducting systems with multi-scale inter-vortex interactions, Journal of Physics: Condensed Matter 25, 415702 (2013). Chosen for IoP Select for quality and recency.
PDFs are available
- local preprint pdf
- arXiv preprint pdf from http://arxiv.org/abs/1212.1130
- Southampton eprints pdf (to be added)
- Journal's pdf (from paper's home page)
This summary of the paper is taken from here.