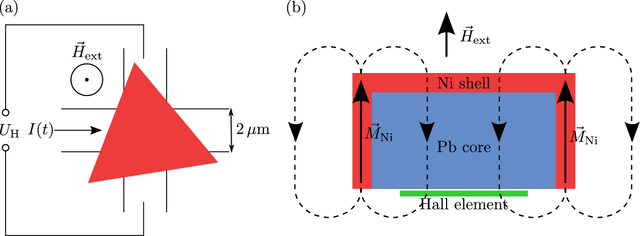
Figure 1: (a) Experimental set-up for measuring the magnetic response of a triangular-platelet shaped Pb/Ni core-shell structure. The structure is placed above a Hall element and the external field is varied along the direction perpendicular to the base of the core-shell structure. From the measured Hall voltage one can infer the spatially averaged magnetic field, the average being taken over the volume of the Hall element. (b) Cross section of the experimental set-up visualising the position of the Hall element below the core-shell structure. It also illustrates that the dominating stray field, which originates from the side walls of the Nickel shells, tends to oppose the external field within the core region.

Figure 2: Hysteresis curve obtained by measuring the spatially averaged magnetic field at the Hall element within a constantly varying external magnetic field. The y-axis shows the measured magnetic field minus the externally applied field. The measurement has been conducted at the Helium boiling temperature of 4.2 K, at which lead is generally superconducting in magnetic fields below a critical field of 530 Oe. Superconducturs behave as ideal diamagnets, i. e. they do not only oppose a magnetic field but completely expel it from their volume. There is a clear superconducting signal at externpal fields between 285 and 970 Oe (indicated by the vertical, dashed lines) when the external field is subsequently decreased (red curve). The oppsite measurement (black curve) leads to an equivalent signal. In the following we refer to this signal as a superconducting dome. Please note that superconductivity exists at external fields well above the actual critical field. As already indicated in Figure 1 (b), this survival of superconductivity at high external field can be interpreted in terms of a partial cancellation between the external field H_ext and the stray field H_stray originating from the side walls of the Nickel shell. In the following this assumption is corroborated by using a simple micromagnetic model.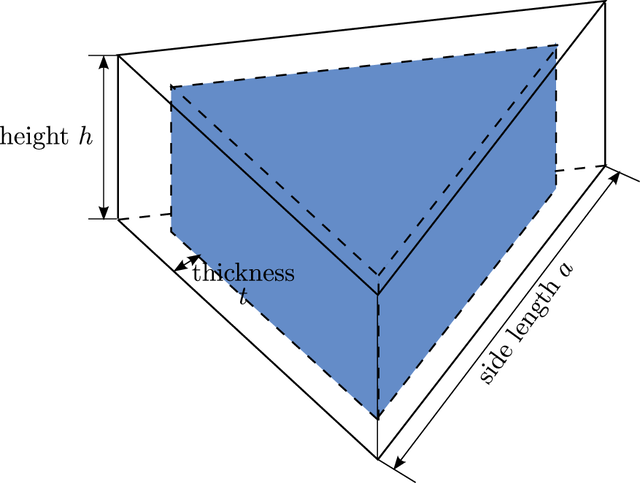

Figure 3: Idealised geometry of the triangular-platlets shaped core-shell structure, on which the computational model is based. The core is shown in a blue color while the shell is translucent. Our micromagnetic model can only describe the magnetc state of the ferromagnetic nickel shell. To numerically solve the corresponding micromagnetic equations the shell region is partitioned by a tetrahedral mesh. The core region is also partitioned by a coarse, tetrahedral mesh in order to probe the magnetic field at its nodes.

Figure 4: The relaxed magnetisation (magnetic dipole density) is illustrated at an external field strength of 1000 Oersted. The latter is perpendicularly aligned with respect to the base of the triangular geometry (see Figure 1). A complex vortex-like configuration is observed. In our model this configuration is kept fixed while the external field is varied. This fixing of the magnetisation models pinning effects, which are present in a realistic sample. For example, such pinning effects may result from the polycrystalline nickel structure or surface roughness.

Figure 5: The superconducting fraction within the lead core is shown at different external fields (at 4.2 K). The data has been obtained as follows: The external field is systematically varied while the magnetisation and thus the resulting magnetic stray field are kept fixed (see Figure 5). At each external field strength the total magnetic field H_total is computed at the mesh nodes which discretizes the volume of the lead core. The total magnetic field is just the sum of the external field H_ext and the stray field H_stray originating from the magnetisation of the side walls (see also the magnetic field lines illustrated in Figure 1 b). If H_total < 530 Oe = H_crit(T=4.2 K) holds at a certain mesh node, lead is assumed to be superconducing in the vicinity of this node. With this approach the superconducting fraction within the lead core is readily determined. Figure 5a to Figure 5g are spatially resolved images of the superconducting material within the core region.

Figure 5a: H_ext = 0 Oe.

Figure 5b: H_ext = 100 Oe.

Figure 5c: H_ext = 300 Oe.

Figure 5d: H_ext = 500 Oe.

Figure 5e: H_ext = 700 Oe.

Figure 5f: H_ext = 900 Oe.

Figure 5g: H_ext = 1200 Oe.